Combinatorial Optimization

Operations Research and Combinatorial Problems

Operations Research (OR) started in the first world war as an initiative to use mathematics and computer science to assist military planners in their decisions. Today, combinatorial optimization algorithms developed in the OR community form the backbone of the most important modern industries including transportation, logistics, scheduling, finance and supply chains.

OR Problems are formulated as integer constrained optimization, i.e., with integral or binary variables (called decision variables). While not all such problems are hard to solve (e.g., finding the shortest path between two locations), we concentrate on Combinatorial (NP-Hard) problems. NP-Hard problems are impossible to solve optimally at large scales as exhaustively searching for their solutions is beyond the limits of modern computers. The Travelling Salesman Problem (TSP) and the Minimum Spanning Tree Problem (MST) are two of the most popular examples for such problems defined using graphs.

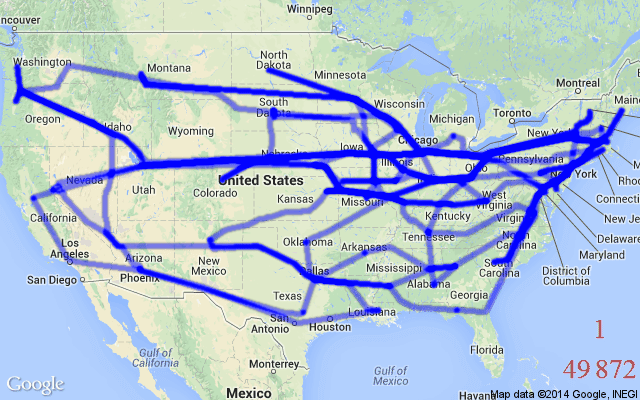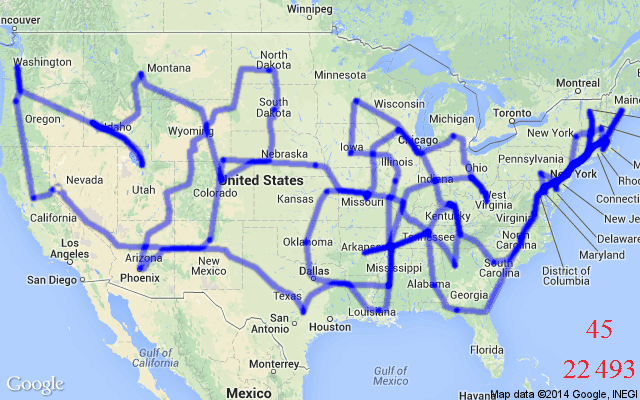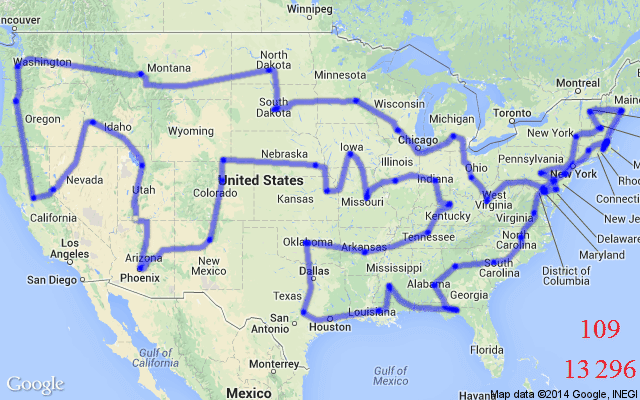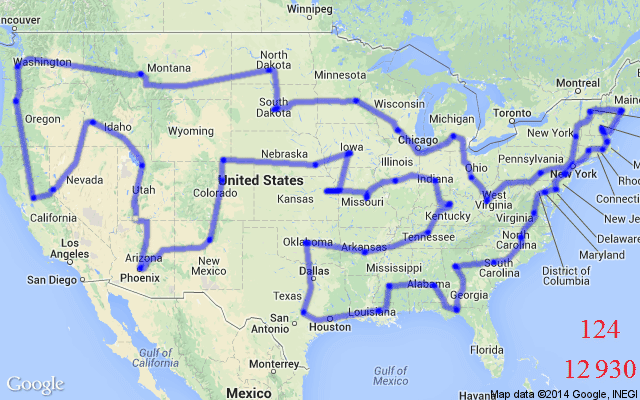TSP asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city? Formally, given a graph, one needs to search the space of permutations to find an optimal sequence of nodes, called a tour, with minimal total edge weights (tour length).

Neural Combinatorial Optimization

Solvers and heuristic algorithms developed in the OR community are able to solve classical problems such as TSP with up to millions of variables. However, designing powerful and robust optimization algorithms requires significant specialized knowledge and years of trial-and-error, especially for understudied but high-impact problems arising in scientific discovery or computer architecture. The state-of-the-art TSP solver, Concorde, leverages over 50 years of research on linear programming, cutting plane algorithms and branch-and-bound.

Since most problems are highly structured, heuristics take the form of rules or policies to make sequential decisions, e.g., determine the TSP tour one city at a time. Our research uses deep neural networks to parameterize these policies and train them directly from problem instances. In particular, Graph Neural Networks are the perfect fit for the task because they naturally operate on the graph structure of these problems.

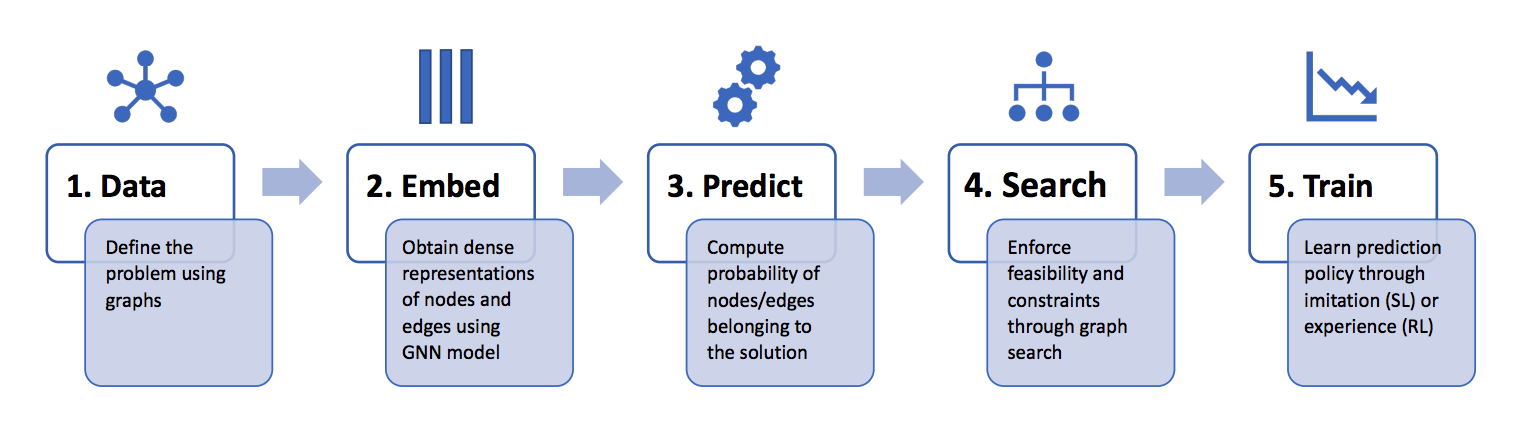A generic five-stage pipeline for end-to-end learning of combinatorial problems on graphs

Why study TSP in particular?

(1) The problem has an amazing history of serving as an engine of discovery for applied mathematics, with several legendary computer scientists and mathematicians having a crack at it. Here’s an amazing talk by William Cook, the co-inventor of the current state-of-the-art Concorde TSP solver.

(2) TSP has been the focus of intense research in the combinatorial optimization community. If you come up with a new solver, e.g., a learning-driven solver, you need to benchmark it on TSP. TSP’s multi-scale nature makes it a challenging graph task which requires reasoning about both local node neighborhoods as well as global graph structure.

(3) Learning-based approaches for heuristic algorithms have the potential to be a breakthrough for OR if they are able to learn efficiently on small scale problems and then generalize robustly to larger instances. However, such scale-invariant generalization is an exciting and unsolved challenge, not just for TSP, but for machine learning as a whole. Update: We explore this in our latest paper!

At the same time, the more profound motivation of using deep learning for combinatorial optimization is not to outperform classical approaches on well-studied problems. Neural networks can be used as a general tool for tackling previously un-encountered NP-hard problems, especially those that are non-trivial to design heuristics for [Bello et al., 2016]. We are excited about recent applications of neural combinatorial optimization for accelarating drug discovery, optimizing operating systems and designing computer chips.

P.S. XB is organizing an exciting workshop at IPAM titled “Deep Learning and Combinatorial Optimization”.