Benchmarking Graph Neural Networks

This blog is based on the paper Benchmarking Graph Neural Networks which is a joint work with Chaitanya K. Joshi, Thomas Laurent, Yoshua Bengio and Xavier Bresson.

Graph Neural Networks (GNNs) are widely used today in diverse applications of social sciences, knowledge graphs, chemistry, physics, neuroscience, etc., and accordingly there has been a great surge of interest and growth in the number of papers in the literature.

However, it has been increasingly difficult to gauge the effectiveness of new models and validate new ideas that generalize universally to larger and complex datasets in the absence of a standard and widely-adopted benchmark.

To address this paramount concern existing in graph learning research, we develop an open-source, easy-to-use and reproducible benchmarking framework with a rigorous experimental protocol that is representative of the categorical advances in GNNs.

Why benchmark?

In any core research or application area in deep learning, a benchmark helps to identify and quantify what types of architectures, principles, or mechanisms are universal and generalizable to real-world tasks and large datasets. Particularly, the recent revolution in this AI field is often credited, to a possibly large extent, to be triggered by the large-scale benchmark image dataset, ImageNet. (Obviously, other driving factors include increase in the volume of research, more datasets, compute, wide-adoptance, etc.)

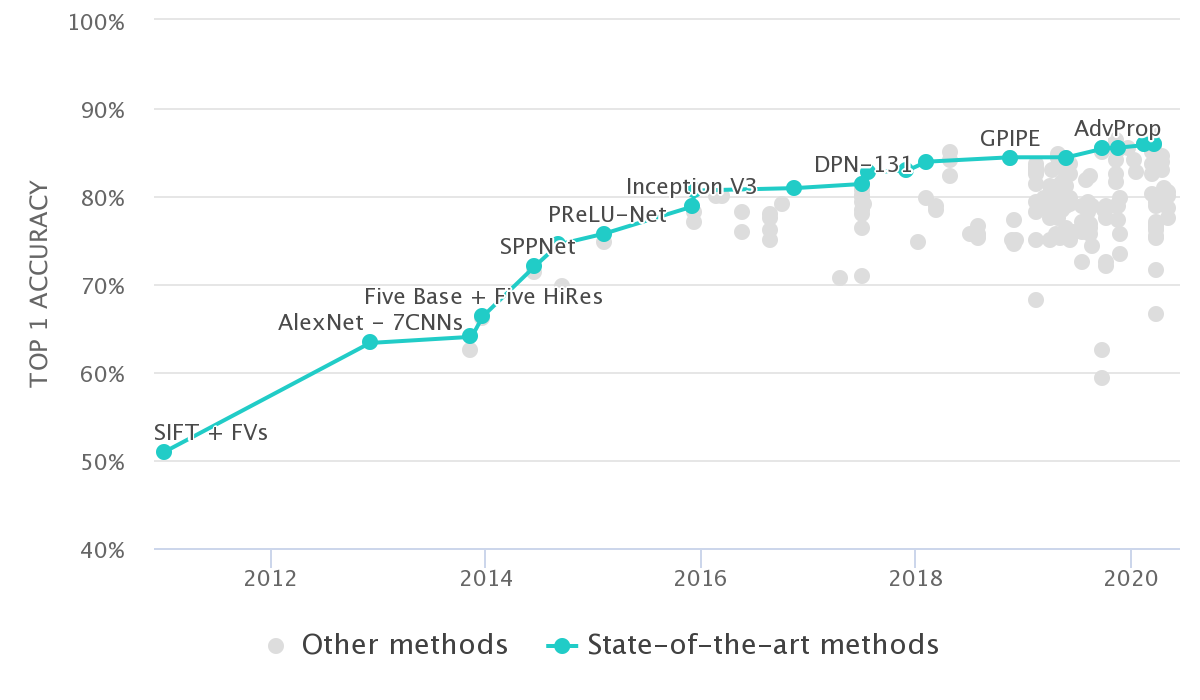
Benchmarking has been proved to be beneficial for driving progress, identifying essential ideas, and solving domain-related problems in many sub-fields of science. This project was conceived with this fundamental motivation.

Need of a benchmarking framework for GNNs

a. Datasets:

Many of the widely cited papers in the GNN literature contain experiments that are evaluated on small graph datasets which have only a few hundreds (or, thousand) of graphs.

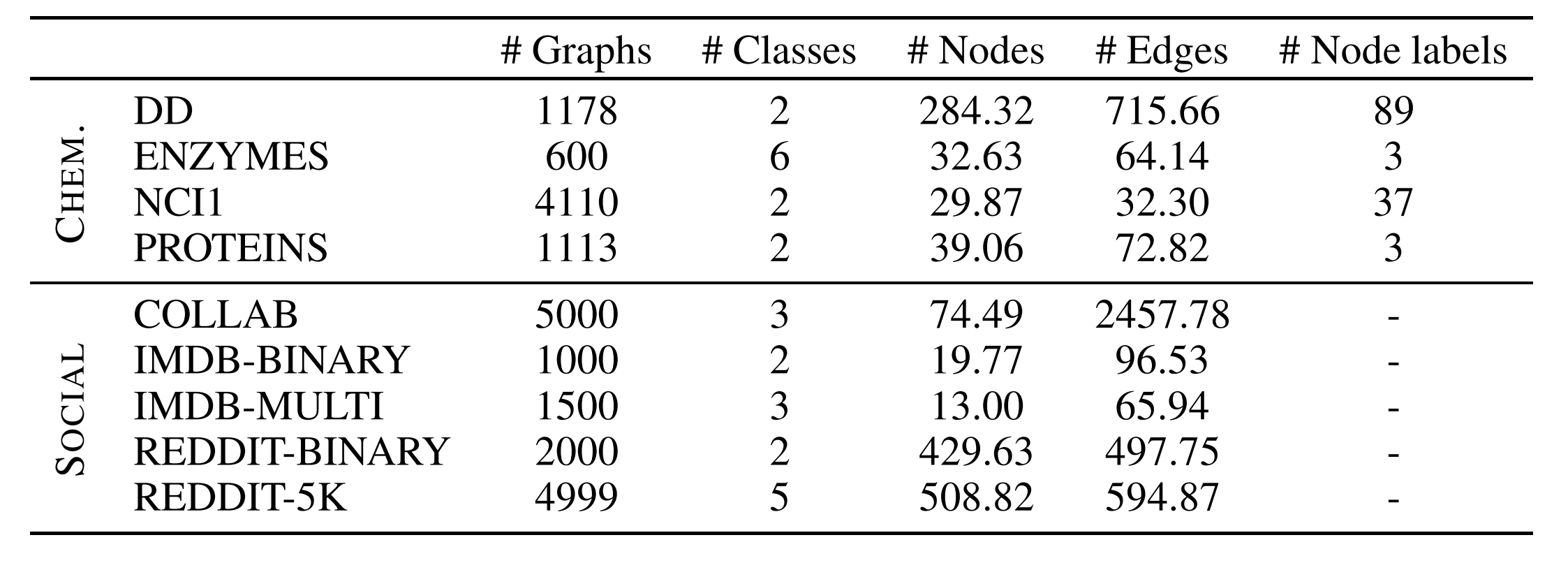
Take for example, the ENZYMES dataset, which is almost seen in every work on a GNN for classification task. If one uses a random $10$-fold cross validation (in most papers), the test set would have $60$ graphs (i.e. $10$% of $600$ total graphs). That would mean a correct classification (or, alternatively a misclassification) would change $1.67$% of test accuracy score. A couple of samples could determine a $3.33$% difference in performance measure, which is usually a significant gain score stated when one validates a new idea in literature. You see there, the number of samples is unreliable to concretely acknowledge the advances. ¹

Our experiments, too, show that the standard deviation of performance on such datasets is large, making it difficult to make substantial conclusions on a research idea. Moreover, most GNNs perform statistically the same on these datasets. The quality of these datasets also leads one to question if you should use them while validating ideas on GNNs. On several of these datasets, simpler models, sometimes, perform as good, or even beats GNNs.

Consequently, it has become difficult to differentiate complex, simple and graph-agnostic architectures for graph machine learning.

b. Consistent experimental protocol:

Several papers in the GNN literature do not have consensus on a unifying and robust experimental setting which leads to discussing the inconsistencies and re-evaluating several papers’ experiments.

For a couple of examples to highlight here, Ying et al., 2018 performed training on $10$-fold split data for a fixed number of epochs and reported the performance of the epoch which has the “highest average validation accuracy across the splits at any epoch” whereas Lee et al., 2019 used an “early stopping criterion” by monitoring the epoch-wise validation loss and report “average test accuracy at last epoch” over $10$-fold split.

Now, if we extract results of both these papers to put together in the same table and claim that the model with the highest performance score is the promising of all, can we get convinced that the comparison is fair?

There are other issues related to hyperparamter selection, comparison in an unfair budgets of trainable paramters, use of different train-validation-test splits, etc.

The existence of such problems pushed us to develop a GNN benchmarking framework which standardizes GNN research and help researchers make more meaningful advances.

Challenges of building a GNN benchmark

The lack of benchmarks have been a major issue in GNN literature as the aforementioned requirements have not been strictly enforced.

Designing benchmarks is highly challenging as we must make robust decisions for coding framework, experimental settings and appropriate datasets. The benchmark should also be comprehensive to cover most of the fundamental tasks which is indicative of the application area the research can be applied to. For instance, graph learning problems include predicting properties at the node-level, edge-level and graph-level. A benchmark should attempt to cover many, if not all, of these.

Similarly, it is challenging to collect real and representative large-scale datasets. The lack of theoretical tools that can define the quality of a dataset or, validate its statistical representativeness for a given task makes it difficult to decide on datasets. Furthermore, there are arbitrary choices required on the features of nodes and edges for graphs and the scale of graph sizes as most of the popular graph learning frameworks do not cater ‘very efficiently’ to large graphs.

There has been a promising effort recently, The Open Graph Benchmark (OGB), to collect meaningful medium-to-large scale dataset in order to steer graph learning research. The initiative is complementary to the goals of this project.

Proposed benchmarking framework:

We propose a benchmarking framework for graph neural networks with the following key characteristics:

1. We develop a modular coding infrastructure which can be used to speed up the development of new ideas
2. Our framework adopts a rigorous and fair experimental protocol,
3. We propose appropriate medium-scale datasets that can be used a plug-ins for later research. ²

4. Four fundamental tasks in graph machine learning are covered, i.e. graph classification, graph regression, node classification, and edge classification.

a. Coding infrastructure:

Our benchmarking code infrastructure is based on Pytorch/DGL.

From a high-level view, our framework unifies independent components for i) Data pipelines, ii) GNN layers and models, iii Training and evaluation functions, iv) Network and hyperparameters configurations, and v) Single execution scripts for reproducibility.

The detailed user instructions on use of each of these components is described on GitHub README. ³

b. Datasets:

We include 8 datasets from diverse domains of chemistry, mathematical modeling, computer vision, combinatorial optimization and social networks.

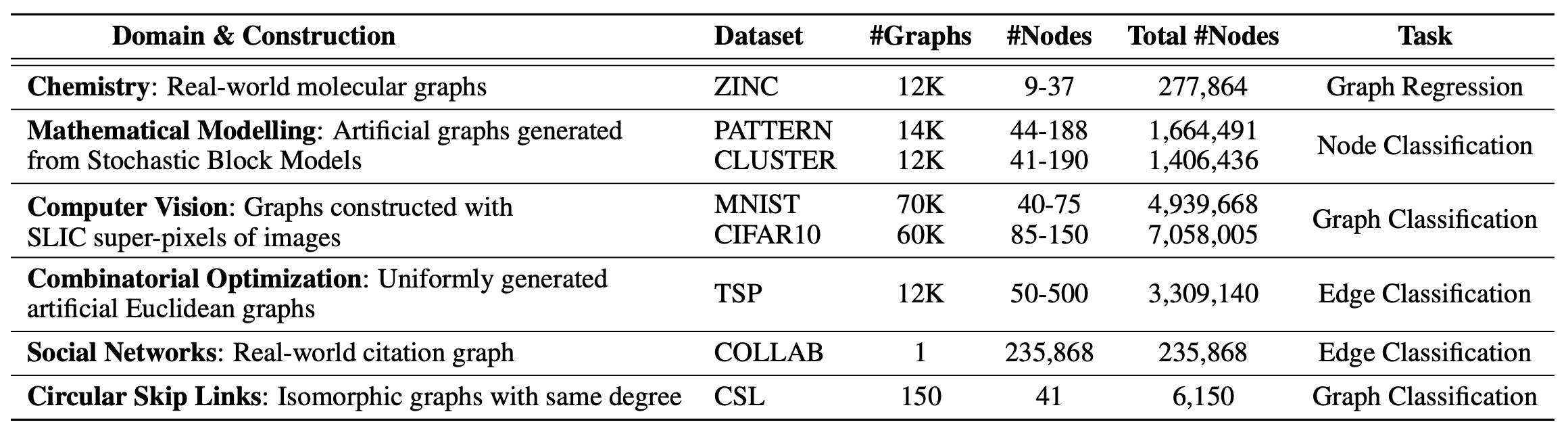
The steps for datasets’ preparation and their relevance to benchmarking graph neural networks are described in the paper.

It is worth mentioning that we include OGBL-COLLAB from OGB which demonstrates the we can flexibly incorporate any of the current and future datasets from the OGB initiative.

c. Experimental Protocol:

We define a rigorous and fair experimental protocol for benchmarking graph neural network models.

Dataset splits: Given the literature has issues with using different train-val-test splits for different models, we make sure our data pipelines provide the same training, validation and test splits for every GNN model compared. We follow standard splits for the datasets available. For synthetic datasets with no standard splits, we ensure the class distribution or the synthetic properties are the same across the splits. Please refer to the paper on more details.

Training: We use the same training setup and reporting protocol for all experiments. We use the Adam optimizer to train the GNNs with a learning rate decay strategy based on the validation loss. We train each experiment for an unspecified number of epochs where the model stops to train at a minimum learning rate at which there is no significant learning.

Importantly, this strategy makes it easy for the users to not fathom on choosing how many epochs to train their model for.

Each experiment is run on $4$ different seeds for a maximum of $12$ hours of training time and the summary statistics of the last epoch score of the $4$ experiments is reported.

Parameter budget: We decide on using two trainable parameter budgets: (i) $100k$ parameters for each GNNs for all the tasks, and (ii) $500k$ parameters for GNNs for which we investigate scaling a model to larger parameters and deeper layers. The number of hidden layers and hidden dimensions are selected accordingly to match these budgets.

We make this choice of having a similar parameter budget for fair comparison because it becomes otherwise difficult to rigorously evaluate different models. In GNN literature, it is often seen the a new model is compared to the existing literature without any detail of the number of parameters, or any attempt to have the same size of the model. Having said that, our goal is not to find the optimal set of hyperparameters for each of the models which is a compute-intensive task.

d. Graph Neural Networks:

We benchmark two broad classes of GNNs that represent the categorical advances in the architectures of a graph neural network witnessed in the most recent literature. We call the two classes, for nomenclature, as GCNs (Graph Convolutional Networks) and WL-GNNs (Weisfeiler-Lehman GNNs).

GCNs refer to the popular message-passing based GNNs which leverage sparse tensor computation and WL-GNNs are the theoretically expressive GNNs based on the WL-test to distinguish non-isomorphic graphs which require dense tensor computation at each layer.

Accordingly, our experimental pipeline is shown in Fig 5 for GCNs and Fig 6 for WL-GNNs.

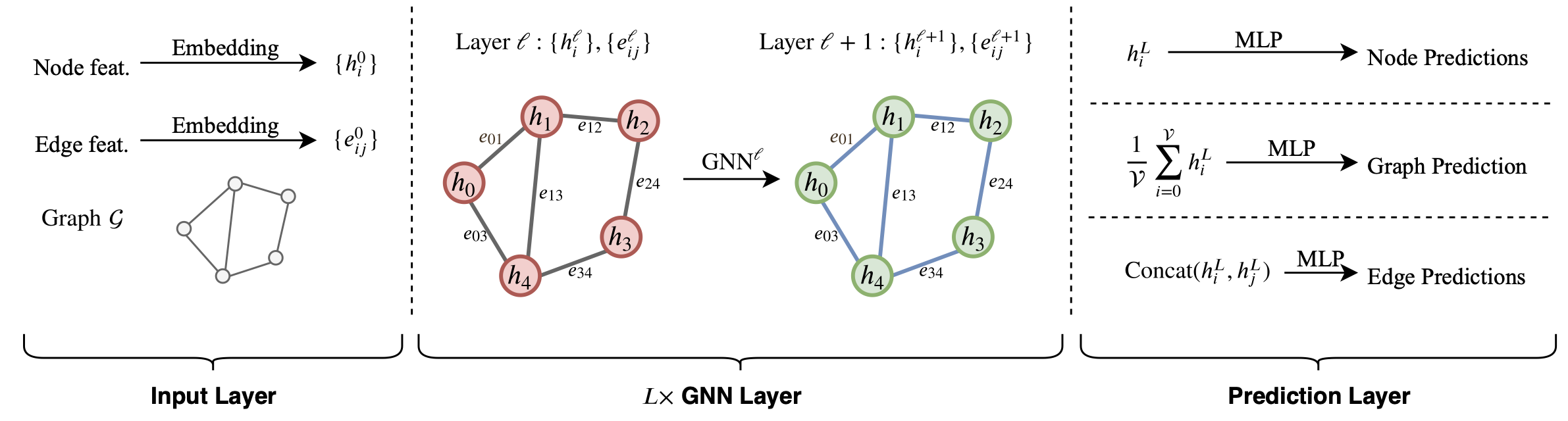
We direct the readers to our paper and the corresponding works for more details on the mathematical formulations of the GNNs. To interested readers, we also include in paper the block diagrams of layer updates of each GNN benchmarked.

We perform a principled investigation into the message passing based GCNs and the WL-GNNs to reveal important insights and highlight critical underlying challenges in building a powerful GNN model.

Benchmarking GNNs on the proposed datasets.

We perform exhaustive experiments on all datasets using every GNN models included currently in our benchmarking framework. The experiments help us draw many insights, few of which are discussed here. We recommend reading the paper for details on the experimental results.

The GNNs that we benchmark are: Vanilla Graph Convolutional Network (GCN), GraphSage, Graph Attention Network (GAT), Gaussian Mixture Model (MoNet), GatedGCN, Graph Isomorphism Network (GIN), RingGNN and 3WL-GNN.

1. Graph-agnostic NNs perform poorly on the proposed datasets: We compare all GNNs to a simple MLP which updates each node’s features independent of one-another, i.e. ignoring the graph structure.

MLP node update equation at layer $\ell$ is: $$ h_{i}^{\ell+1} = \sigma \left( W^{\ell} \ h_{i}^{\ell} \right) $$

MLP evaluates to consistently low scores on each of the datasets which shows the necessity to consider graph structure for these tasks. This result is also indicative of how appropriate these datasets are for GNN research as they statistically separate model’s performance.

2. GCNs outperform WL-GNNs on the proposed datasets: Although WL-GNNs are provably powerful in terms of graph isomorphism and expressiveness, the WL-GNN models that we consider were not able to outperform GCNs. These models are limited in scaling to larger datasets as their space/time complexity are inefficient as compared to the GCNs which leverage sparse tensors.

GCNs are seen to conveniently scale to $16$ layers and provide the best results on all datasets, whereas the WL-GNNs face loss divergence and/or out-of-memory errors when trying to build deeper networks.

3. Anisotropic mechanisms improve message-passing GCNs architectures: Among the models in the message-passing GCNs, we can classify them into isotropic and anisotropic.

A GCN model whose node update equation treats every edge direction equally, is considered isotropic; and a GCN model whose node update equation treats every edge direction differently, is considered anisotropic.

Isotropic layer update equation: $$ h_{i}^{\ell+1} = \sigma \Big( W_1^{\ell} \ h_{i}^{\ell} + \sum_{j \in \mathcal{N}_i} W_2^{\ell} \ h_{j}^{\ell} \Big) $$

Anisotropic layer update equation: $$ h_{i}^{\ell+1} = \sigma \Big( W_1^{\ell} \ h_{i}^{\ell} + \sum_{j \in \mathcal{N}_i} \eta_{ij} W_2 h_{j}^{\ell} \Big) $$

As per the above equations, GCN, GraphSage and GIN are isotropic GCNs whereas GAT, MoNet and GatedGCN are anisotropic GCNs.

Our benchmark experiments reveal that the anisotropic mechanism is an architectural improvement in GCNs which give consistently impressive results. Note that sparse and dense attention mechanisms (in GAT and GatedGCN respectively) are examples anisotropic components in a GNN.

4. There are underlying challenges for training the theoretically powerful WL-GNNs: We observe a high standard deviation of performance scores on the WL-GNNs. (Recall that we report every performance of 4 runs with different seeds). This reveals the problem in training these models.

Universal training procedures like batched training and batch normalization are not used in WL-GNNs since they operate on dense rank-2 tensors.

To describe this clearly, the batching approach for GCNs in leading graph machine learning libraries which operate on sparse rank-2 tensors involves preparing a sparse block diagonal adjacency matrix for a batch of graphs.

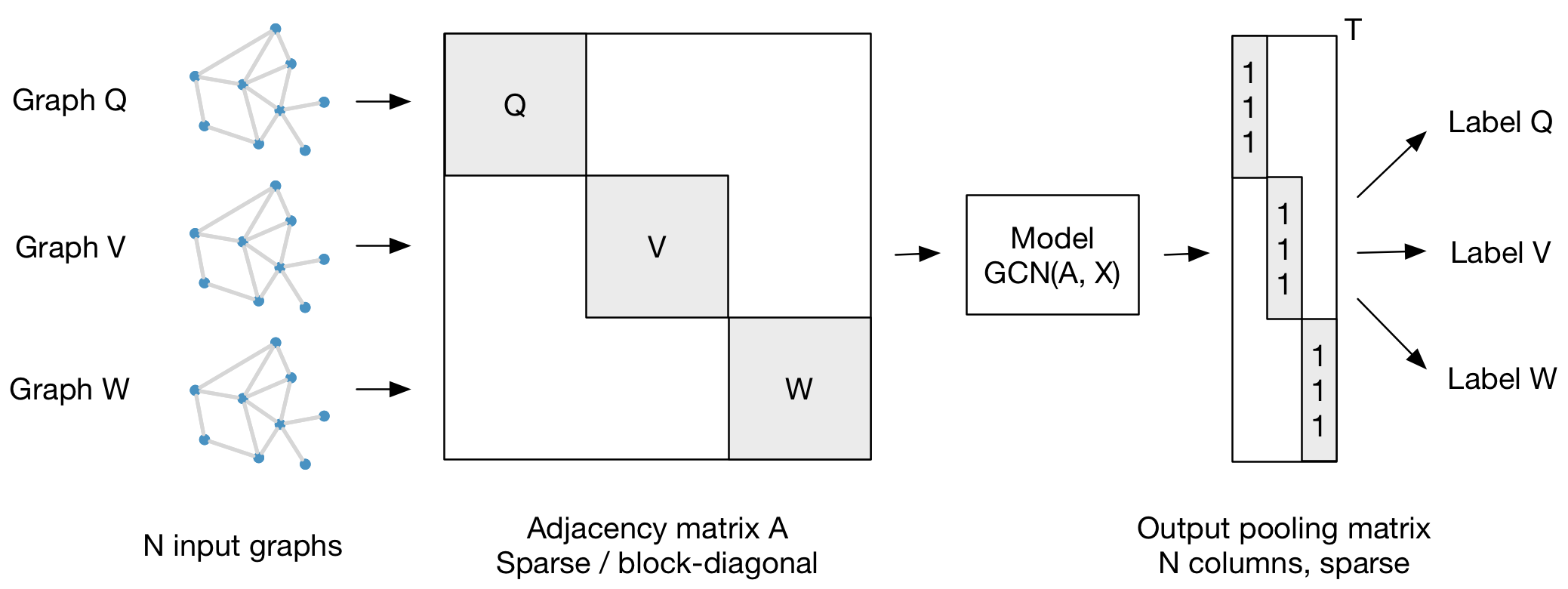
The WL-GNNs that operate on dense rank-2 tensors, have components which compute information at/from every position in the dense tensor. Therefore, the same approach (Fig 7) is not applicable as it would make the entire block diagonal matrix dense and would break sparsity.

GCNs leverage batched training and hence batch normalization for stable and fast training. Besides, WL-GNNs, with the current design, are not suitable for single large graphs, eg. OGBL-COLLAB. We failed to fit the dense tensor of this large size on both GPU and CPU memory.

Hence, our benchmark suggests the need for re-thinking better design approaches for WL-GNNs which can leverage sparsity, batching, normalization schemes, etc. that have become universal ingredients in deep learning.

More reading

With this introduction and usefulness of a GNN benchmarking framework, we conlcude this blog post, but there is more reading left if you’re interested in this work.

Particularly, we investigate anisotropy and edge representations for link prediction in more detail in the paper and propose a new approach for improving low-structurally expressive GCNs. We shall discuss these in future blog posts separately for clear understanding.

If this benchmarking framework comes to use in your research, please use the following bibtex in your work. For discussions, hit us with a query on GitHub Issues. We would love to discuss and improve the benchmark for steering more meaningful research in graph neural networks.

@article{dwivedi2020benchmarkgnns,
  title={Benchmarking Graph Neural Networks},
  author={Dwivedi, Vijay Prakash and Joshi, Chaitanya K and Laurent, Thomas and Bengio, Yoshua and Bresson, Xavier},
  journal={arXiv preprint arXiv:2003.00982},
  year={2020}
}