Residual Gated Graph ConvNets

Abstract

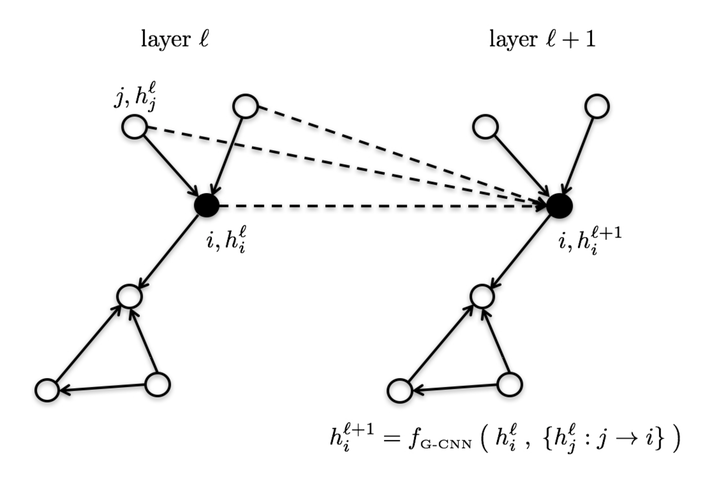
Graph-structured data such as social networks, functional brain networks, gene regulatory networks, communications networks have brought the interest in generalizing deep learning techniques to graph domains. In this paper, we are interested to design neural networks for graphs with variable length in order to solve learning problems such as vertex classification, graph classification, graph regression, and graph generative tasks. Most existing works have focused on recurrent neural networks (RNNs) to learn meaningful representations of graphs, and more recently new convolutional neural networks (ConvNets) have been introduced. In this work, we want to compare rigorously these two fundamental families of architectures to solve graph learning tasks. We review existing graph RNN and ConvNet architectures, and propose natural extension of LSTM and ConvNet to graphs with arbitrary size. Then, we design a set of analytically controlled experiments on two basic graph problems, ie subgraph matching and graph clustering, to test the different architectures. Numerical results show that the proposed graph ConvNets are 3-17% more accurate and 1.5-4x faster than graph RNNs. Graph ConvNets are also 36% more accurate than variational (non-learning) techniques. Finally, the most effective graph ConvNet architecture uses gated edges and residuality. Residuality plays an essential role to learn multi-layer architectures as they provide a 10% gain of performance.